Normal-guided Detail-Preserving Neural Implicit Function for High-Fidelity 3D Surface Reconstruction
Abstract
Neural implicit representations have emerged as a powerful paradigm for 3D reconstruction. However, despite their success, existing methods fail to capture fine geometric details and thin structures, especially in scenarios where only sparse multi-view RGB images of the objects of interest are available. In this paper, we show that training neural representations with first-order differential properties (surface normals) leads to highly accurate 3D surface reconstruction, even with as few as two RGB images. Using input RGB images, we compute approximate ground truth surface normals from depth maps produced by an off-the-shelf monocular depth estimator. During training, we directly locate the surface point of the SDF network and supervise its normal with the one estimated from the depth map. Extensive experiments demonstrate that our method achieves state-of-the-art reconstruction accuracy with a minimal number of views, capturing intricate geometric details and thin structures that were previously challenging to capture.
Overview
An overview of our method. Our method involves the following steps: (a) We cast camera rays from each pixel into the scene while sampling \(m\) points along the ray. (b) For each sampled point, we find the corresponding SDF \(\hat{q}\) and rendered RGB color \(\hat{c}\) using an SDF and Neural Renderer network, respectively. Then we use volume rendering in a differentiable manner to find the rendered color for each pixel. (c) Finally, we additionally supervise our network with Depth-Normal Consistency loss that enables the 3D reconstruction of intricate geometric details and thin structures.
Rendering Results
Novel view synthesis: Examples of RGB images and their corresponding normal maps rendered, using our approach, from novel views.
Reconstruction Results
Comparison on the DiLiGenT-MV dataset with 2 input views (front and back): Ours (mono-illumination) vs PS-NeRF [ECCV 2022] (multi-illumination) vs NeuS [NeurIPS 2021] (mono-illumination).
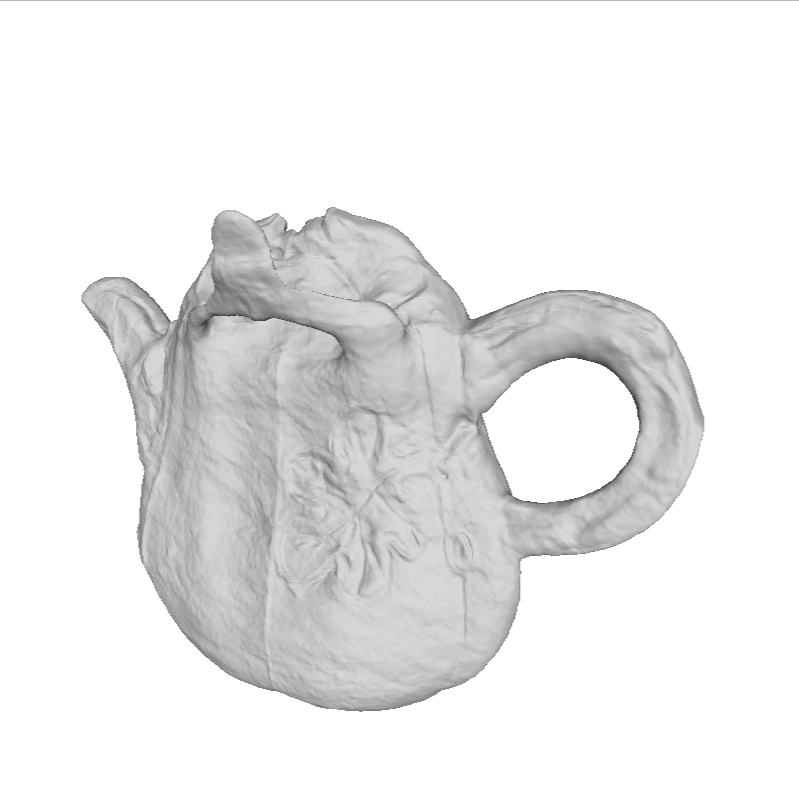
Comparison with SOTA on the DiLiGenT-MV dataset with different number of input views: Ours (mono-illumination) vs Super Normal [CVPR 2024] (multi-illumination) vs RNb-NeuS [CVPR 2024] (multi-illumination).
Comparison with Gaussian Surfels [SIGGRAPH 2024] (SOTA) on the BMVS dataset with all input views setting.
Comparison with Gaussian Surfels [SIGGRAPH 2024] (SOTA) on the DTU dataset with sparse (three) input views setting.
